People involved in the design, construction and operation of large dams are normally particularly sensitive to earthquakes.
This is because of four factors:
- Dams are often built in active earthquake areas
- Reservoirs can trigger earthquakes
- Some water supply structures are susceptible to earthquake motion.
Embankments and outlet towers respond to earthquake vibrations. Shaking an unstable slope that has been weakened after saturation by rises in ground water levels may produce a landslide into the reservoir. - The consequence of a dam or water supply failure is high.
The effects of a dam failure on people and structures downstream are dramatic and obvious. A more likely example of earthquake damage would be loss of control of the water supply.
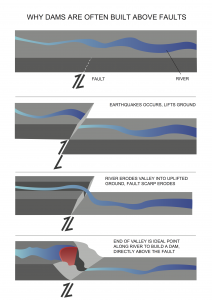 Why are Dams Often Built in Active Earthquake Areas?
Why are Dams Often Built in Active Earthquake Areas?
- Dams are usually built in valleys
- Valleys exist because active erosion is taking place
- Active erosion implies there has been recent uplift
- Under compressional tectonic force, reverse or thrust faults produce uplift
- Reverse or thrust faults dip under the upthrown block
- Therefore, many dams have an active fault dipping under them
Reservoir Triggered Earthquakes
Large new reservoirs can trigger earthquakes. This is due to either:
- change in stress because of the weight of water, or more commonly by
- increased groundwater pore pressure decreasing the effective strength of the rock under the reservoir.
For triggered earthquakes to occur, both mechanisms require that the area is already under considerable tectonic stress.
Reservoir triggered earthquakes are often referred to as reservoir induced seismicity (RIS), but use of the term “induced” is now becoming unfashionable. To many people it implies that the reservoir caused the earthquake. The energy released in a reservoir triggered earthquake is normal tectonic strain energy that has been prematurely released because of the reservoir.
Water Pore Pressure
Ground water plays a large part in earthquake activity. Fluid injection into wells in USA, Japan and elsewhere has triggered small earthquakes.
Water pore pressure reduces the normal stress within a rock while not changing the shear stress. Under any circumstances, an increase in water pore pressure means that a failure is more likely. The critical value of shearing stress may be made arbitrarily low by increasing the pore pressure.
Pore pressure can increase in two ways:
- Due to the decrease in pore volume caused by compaction under the weight of the reservoir. This occurs while the reservoir is being filled.
- Due to diffusion of reservoir water through permeable rock under the reservoir. The rate of flow depends on the permeability of the rock, so this effect is not instantaneous. The increase in pore pressure takes more time depending on the distance from the reservoir. It may take years for the pore pressure to increase at depths of kilometres beneath a reservoir.
Examples of Reservoir Triggered Earthquakes
World
- Koyna, India, 1967, M 6.7
- Xinfengjiang, China, 1962, M 6.2
Australia
- Warragamba, NSW, 1973, ML 5.5
- Thomson, Victoria, 1996, ML 5.1
Duration of Reservoir Triggered Seismicity
Reservoir induced seismicity is a transitory phenomenon which will occur either immediately after filling of the reservoir, or after a delay of a few years. If there is a delay, this depends on the permeability of the rock beneath the reservoir.
Once stress and pore pressure fields have stabilised at new values, reservoir induced seismicity will cease. Earthquake hazard will then revert to similar levels that would have existed if the reservoir had not been filled.
Even for those reservoirs that show a correlation between earthquake activity and water level, reservoir induced seismicity does not continue indefinitely as it is limited by the available tectonic energy.
Depth of Reservoir Triggered Seismicity
Depths of reservoir induced earthquakes, especially those occurring immediately after filling of the reservoir, are normally very shallow. If detailed seismograph coverage is available, then depths within one to three kilometres of the surface are common.
Induced earthquakes at reservoirs that have experienced delayed triggering may be much deeper, perhaps as deep as ten to twenty kilometres. These may occur ten to twenty years after filling of the reservoir.
Prediction of Reservoir Triggered Seismicity
It is not easy to predict whether a new reservoir will experience reservoir induced seismicity, because the two most important factors – the state of stress and the rock strength at earthquake depths – cannot be measured directly.
This is the same reason why prediction of normal (non-induced) earthquakes is normally unsuccessful.
