How we compare earthquake size to Richter’s original scale.
Charles Richter originally developed a scale to categorise the energy released from earthquakes in California as recorded on a Wood-Anderson torsion seismograph. A magnitude Zero earthquake was defined as one that generated 1 micrometer of horizontal displacement at 100km from the earthquake’s epicentre. This is why you can have negative magnitude earthquakes. It is a logarithmic scale, so one magnitude unit is 10 times bigger than the last.
This scale has been adapted to work in different parts of the world, using different types of seismographs, and for earthquakes that occur at various distances. Today, the vertical velocity of the ground (rather than horizontal displacement) is used as the basis for magnitude calculations. A good summary of the adaptations and formulae are available on Wikipedia (photo source).
Since the SRC started monitoring earthquakes in 1976, we have used a standard Richter-method formula to calculate earthquake magnitudes, using a function to replicate the look-up table traditionally used to compensate for the distance of the earthquake from the seismograph. We have referred to this type of magnitude as ML (magnitude, local) but a more accurate definition is MLv (magnitude, local, using vertical displacement).
In the days when we used paper records and velocity sensors, we would need to convert the recorded peak ground velocity to a peak ground displacement, which is done mathematically by using the frequency of the velocity signal. This was a valid but less-accurate way of determining the peak displacement, but it has been used consistently by the SRC for almost 40 years. Geoscience Australia also uses a vertical-displacement-based formula to calculate ML, but for the last few years GA have been using their own coefficients to compensate for signal attenuation over distance, which varies for different parts of Australia. In the east Australian zone, GA’s coefficients tend to produce slightly lower magnitudes that the SRC’s formula, contributing to differences discussed here.
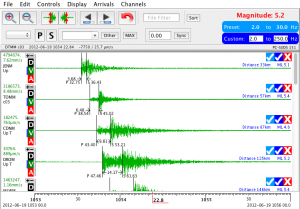In the latest version of eqWave (supplied free with any Kelunji seismograph) we automatically convert the entire waveform recording from velocity to displacement to get the true peak displacement value. By picking a P wave and S wave arrival, eqWave will automatically estimate the distance of the earthquake and display the calculated MLv magnitude. If eqWave is displaying multiple stations that have recorded the same earthquake, eqWave will display an average of all of the calculated magnitudes.
With the distance from each station to the earthquake displayed, and the P-wave and S-wave velocities customisable for different parts of the world, eqWave is very close to becoming a simple earthquake location utility like our iPad app, Quick Quake. Stay tuned for further developments!